Estrutura dos cristais, Cristaloquímica e Regras de Pauling

Estrutura Cristalina

A estrutura de um cristal é a manifestação macroscópica de suas características físicas e químicas. Os átomos e íons que o compõe são ordenados e empacotados, formando diferentes tipos de ordenamento atômico.

Entender a estrutura dos materiais cristalinos é fundamental para entender propriedades de clivagem, dureza, densidade, ponto de fusão e propriedades ópticas, como o índice de refração.

Coordenação de íons

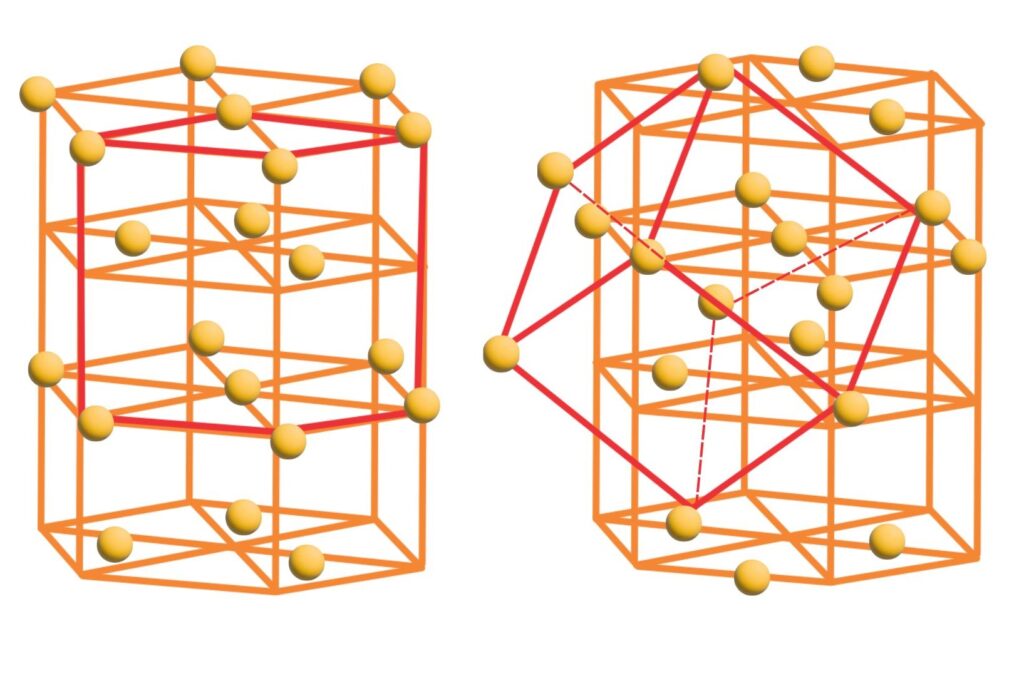
Átomos agrupam-se em um arranjo ordenado que minimiza espaços vazios. Diferentes arranjos são feitos de acordo com variações nos íons, principalmente de acordo com suas cargas e raio iônicos (tamanho). Assume-se que esses íons apresentam o mesmo tamanho, formato esférico e são agrupados como bolas de gude ou tênis.

Exemplos:

Empacotamento hexagonal fechado

Empacotamento cúbico fechado

Regras de Pauling

Nas estruturas cristalinas existem espaços vazios (interstícios) que podem acomodar esferas menores. Muitos minerais são compostos por diversos elementos com tamanho iônico/atômico variado. Assim, podemos considerar que as estruturas minerais consistem de esferas de diferentes tamanhos, empacotadas em um arranjo conjunto.

Geralmente, os ânions formam o empacotamento mais fechado (preenchendo mais espaço), enquanto os cátions (com menores raios iônicos e tamanho), preenchem os espaços vazios nesses arranjos. Assim, surgem questões como:

1. Quais cátions podem caber nesses espaços?
2. Quais são os íons vizinhos?

Linus Pauling tratou dessas questões e compreendeu que uma estrutura cristalina estável resulta de regras básicas. Essas regras foram apresentadas em 1929 e são conhecidas como as Regras de Pauling.

O principio da Coordenação

Um poliedro de ânions forma-se em torno de cada cátion. A distância cátion-ânion é dada pela soma dos raios, enquanto o número de coordenação (número de vizinhos mais próximos) do cátion é determinado pela razão entre os raios.

Este princípio estabelece que os tamanhos relativos dos íons determina como eles se empacotam. Assim, o íon coordena seus vizinhos mais próximos. Os íons coordenados sempre se agrupam ao redor de um íon central, fazendo com que seus centros estejam nos centros do poliedro de coordenação (tetraedro, octaedro, etc.). Geralmente, ânions se agrupam ao redor de cátions. O número de ânions circundando o cátion central do poliedro é o número de coordenação (NC) catiônico em relação ao ânion.

O NC, e consequentemente o arranjo geométrico, são formados em função dos tamanhos relativos dos íons. O tamanho relativo é expresso como relação dos raios:

Relação dos raios = R_cátion / R_ânion

Exemplo:

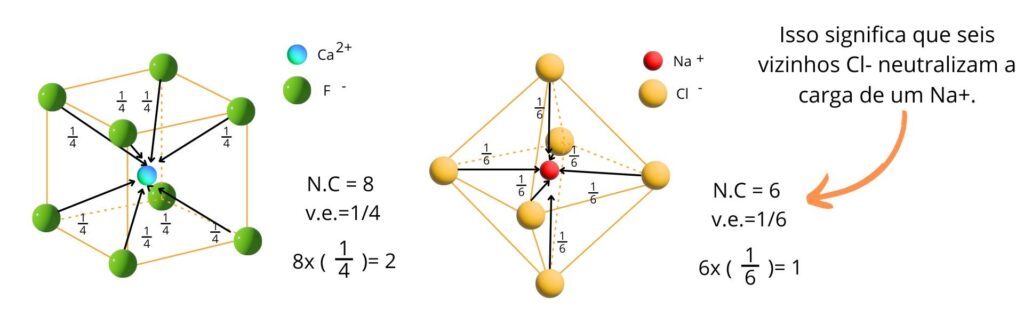
Fluorita

R_Ca²⁺ = 1.12 Å

R_F^– = 1.31 Å

R_Ca²⁺ / R_F^– = 1.12 / 1.31 = 0.86

A razão entre os raios determinará o NC e o poliedro de coordenação.

Os poliedros regulares apresentam números de coordenação:

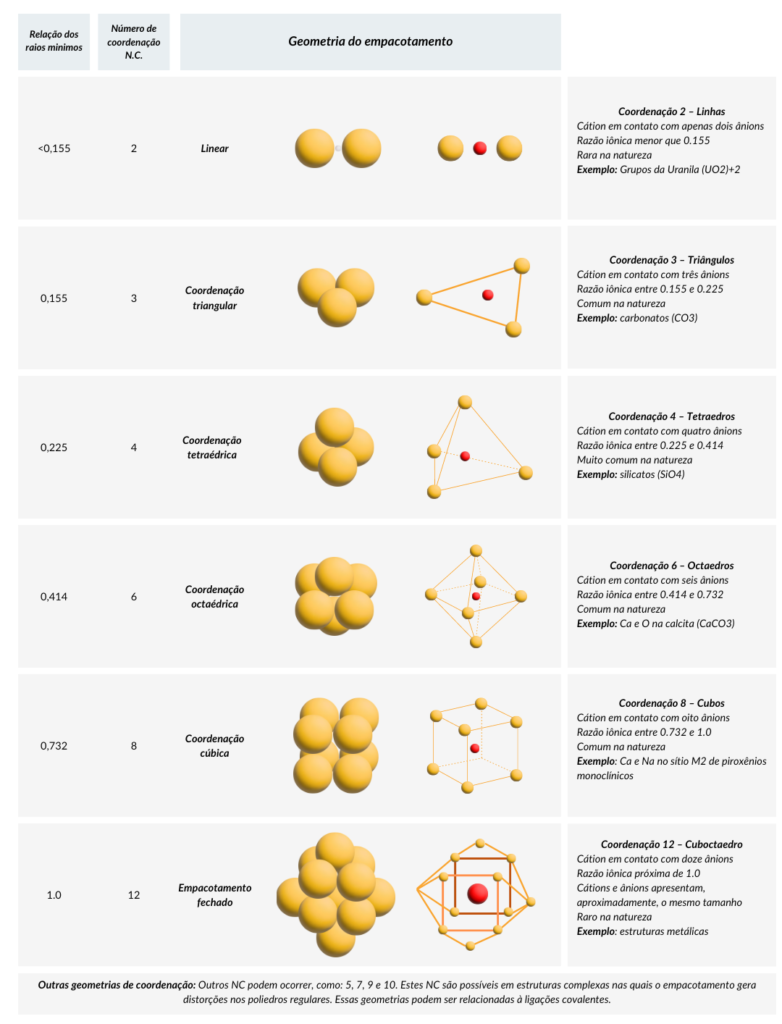
Coordenação 2 – Linhas

Cátion em contato com apenas dois ânions

Razão iônica menor que 0.155

Rara na natureza

Exemplo: Grupos da Uranila (UO₂)⁺²

      Coordenação 3 – Triângulos

                  Cátion em contato com três ânions

                  Razão iônica entre 0.155 e 0.225

                  Comum na natureza

                  Exemplo: carbonatos (CO₃)

Coordenação 4 – Tetraedros

                  Cátion em contato com quatro ânions

                  Razão iônica entre 0.225 e 0.414

                  Muito comum na natureza

                  Exemplo: silicatos (SiO₄)

      Coordenação 6 – Octaedros

                  Cátion em contato com seis ânions

                  Razão iônica entre 0.414 e 0.732

                  Comum na natureza

                  Exemplo: Ca e O na calcita (CaCO₃)

      Coordenação 8 – Cubos

                  Cátion em contato com oito ânions

                  Razão iônica entre 0.732 e 1.0

                  Comum na natureza

                  Exemplo: Ca e Na no sítio M2 de piroxênios monoclínicos

      Coordenação 12 – Cuboctaedro

Cátion em contato com doze ânions

                  Razão iônica próxima de 1.0

                  Cátions e ânions apresentam, aproximadamente, o mesmo tamanho

                  Raro na natureza

                  Exemplo: estruturas metálicas

Outras geometrias de coordenação

Outros NC podem ocorrer, como: 5, 7, 9 e 10.

Estes NC são possíveis em estruturas complexas nas quais o empacotamento gera distorções nos poliedros regulares. Essas geometrias podem ser relacionadas à ligações covalentes.

Coordenação de cátions comuns

Íon	Número de coordenação com oxigênio		Raio iônico em Å
O2-			1,36
K+	8 – 12	Cúbica a Cúbicoctaédrica	1,51 – 1,64
Na+	8 – 6	Cúbica a Octaédrica	1,18 – 1,02
Ca2+	8 – 6		1,12 – 1,00
Mn2+	6	Octaédrica	0,83
Fe2+	6		0,78
Mg2+	6		0,72
Fe3+	6		0,65
Ti4+	6		0,61
Al3+	6		0,54
Al3+	4	Tetraédrica	0,39
Si4+	4		0,26
P5+	4		0,17
S6+	4		0,12
C4+	3	Triangular	-0,08

O princípio da valência eletrostática

Em uma estrutura cristalina estável, a força total das ligações iônicas que alcançam um ânion a partir de todos os cátions vizinhos é igual à carga do ânion.

Essa regra expressa a força de ligação iônica, sendo definida como a carga de valência de um íon (Z) dividida pelo seu NC.

Valência eletrostática (VE) = carga do íon (Z) / número de coordenação (NC)

Exemplo:

NaCl

Neste caso, o íon Cl^– é circundado por seis Na⁺ vizinhos e sua coordenação é octaédrica (NC = 6), portanto, cada uma da ligações com o Na⁺ tem VE igual a:

VE_Na = carga do íon / número de coordenação

Carga Na⁺ = 1

NC_Na = 6

VE = 1 / 6

Isso significa que seis vizinhos Cl^– neutralizam a carga de um Na⁺.

A VE é a mesma para o Cl- (1/6), já que seu NC é 6 e sua carga é igual a do Na⁺ (em módulo).

OBSERVAÇÃO: é importante lembrar que o cáclulo da VE deve ser sempre feito em módulo, sem considerar valores negativos. Exemplo: VE_Cl^– = 1/6. O valor -1/6 está errado.

Compartilhamento de elementos poliédricos I

A existência de arestas e faces comuns a dois poliedros aniônicos em uma estrutura, diminui a estabilidade das estruturas iônicas.

Portanto, o compartilhamento de vértices, arestas ou faces leva a instabilidade.

Essa regra é um lembrete de que cátions gostam de estar o mais afastados quanto possível.

Lembre-se: cada íon produz um efeito na estrutura cristalina.

Se forem iguais: se repelem;

Se forem diferentes: se atraem

A estrutura cristalina tende a se agrupar de forma que os cátions fiquem o mais longe possível um dos outros, enquanto os ânions se coordenam visando a neutralidade elétrica.

Assim, os poliedros de coordenação que vimos anteriormente são conectados e compartilham arestas e vértices, mas raramente faces. Isso acontece porque o compartilhamento de faces deixaria íons de carga simila muito próximos um dos outros.

Exemplo:

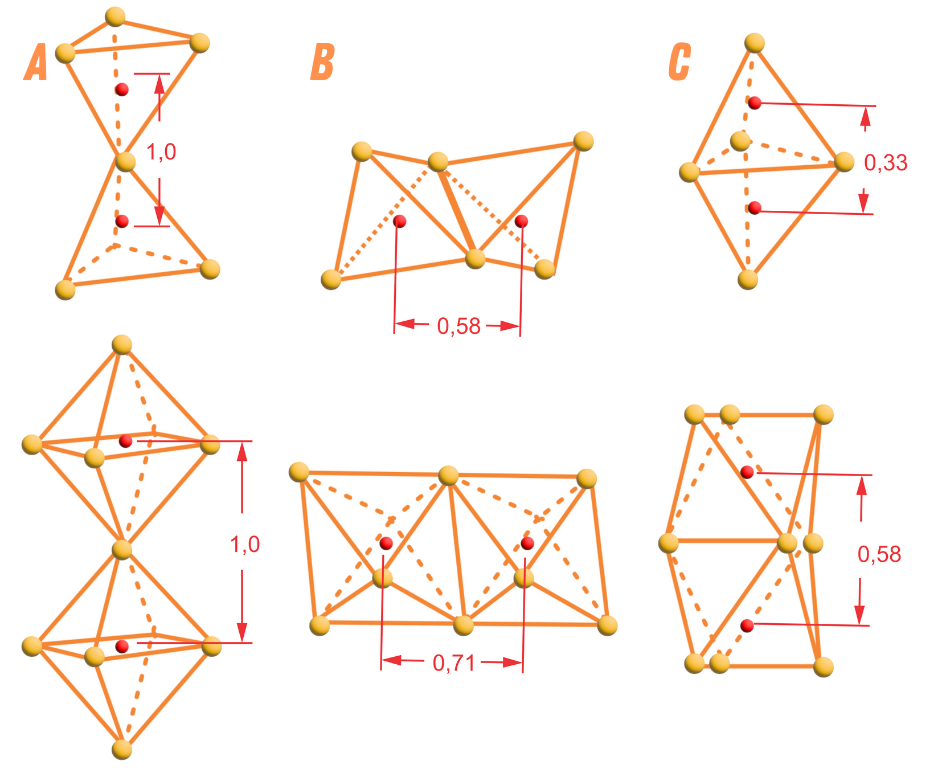
Se dois octaedros são ligados por um oxigênio compartilhado, a distância máxima entre os centros dos cátions é igual a 1,0.

Caso eles compartilhem arestas, essa distância cai para 0,71.

No caso do compartilhamento de faces, a distância entre os centros é ainda mais reduzida, agora para 0,58.

Compartilhamento de elementos poliédricos II

Em um cristal com diferentes cátions, aqueles de alta carga (valência) e pequeno número de coordenação tendem a não compartilhar elementos poliédricos. Assim, a distância entre os cátions atinge um valor máximo, como na Regra 3.

As regras 1 a 4 refletem a tendência de que estruturas cristalinas maximizam as atrações cátion-ânion e minimizar as repulsões cátion-cátion, ânion-ânion.

Princípio da parcimônia

O número de tipos constituintes diferentes de um cristal tende a ser pequeno, pois existem poucos sítions iônicos diferentes na estrutura cristalina.

Assim, estruturas complexas podem apresentar diferentes íons ocupando a mesma posição estrutural (sítio cristalino). Esses íons são considerados como um único “constituinte”, gerando a chamada solução sólida.

Exemplo:

Anfibólios

Os anfibólios apresentam um número limitado de sítios cristalográficos, mas grande variação na composição química. Seus 5 sítios cristalográficos são:

1. Tetraédricos (T1 e T2)

                     Si⁺⁴ e Al⁺³

1. Octaédricos (M1, M2 e M3)

                     Mg⁺², Fe⁺², Mn⁺², Al⁺³, Fe⁺³ e Ti⁺⁴

1. Cúbica (M4)

                     Mg⁺², Mn⁺², Fe⁺², Ca⁺² e Na⁺

1. Sítio A – grande e com NC irregular

                     Na⁺ ou K⁺

• Posição (OH)^–

                     Cl^– ou F^–

Isoestruturalismo

Quando minerais apresentam o mesmo tipo de estrutura, são chamados de isoestruturais ou isotípicos. Este é o caso entre a Uraninita (UO₂) e a Fluorita (CaF₂).

A estrutura da Uraninita apresenta quatro ânions U⁺⁴ em torno de cada oxigênio, com oito oxigênios O^-2 se agrupando em torno de cada U⁺⁴.

Na Fluorita, quatro íons Ca⁺² se agrupam em torno de cada flúor, enquanto oito íons F^– estão empacotados ao redor de cada Ca⁺².

Cristais em que os centros dos átomos ocupam posições geometricamente similares pertencem ao mesmo tipo de estrutura.

Grupos isostruturais são grupos de minerais relacionados por suas estruturas semelhantes, geralmente apresentando um ânion comum, mas cátions diferentes.

OBSERVAÇÃO: Algumas vezes, o termo isomórfo/isomorfismo é utilizado em vez de isoestruturalismo, o que não é recomendado.

Polimorfismo

Em alguns casos, quando o NC está próximo de um valor limite entre os poliédros de coordenação (p. ex. 1,51; 1,00), o cátion pode pertencer a dois poliedros de coordenação diferente.

Assim, o mesmo cátion pode formar, por exemplo, poliedros cúbicos e octaédricos se a razão cátion/ânion for próxima de 1,0.

Exemplo:

CaCO₃ – Calcita

Ca/O tem uma relação de raios de 0,714, muito próximo do limite 0,732 para transformação da coordenação 6 para coordenação 8. Consequentemente, o Ca pode ocorrer em dois tipos de estrutura.

Na Calcita, o Ca apresenta coordenação 6 com o oxigênio, enquanto que na aragonita (CaCO₃), o cálcio está em coordenação 9 com o oxigênio.

Quando dois minerais têm a mesma fórmula química, mas diferentes estruturas, são denominados polimorfos.

Referências

Klein, C., & Dutrow, B. (2009). Manual de ciência dos minerais. Bookman Editora.

Dana, J. D. (1978). Manual de Mineralogia (5º edição). Revisto por Hurlbut Jr., CS Tradução: Rui Ribeiro Franco. Livros Técnicos e Científicos Editora SA, Rio de Janeiro, Brasil.

Nesse, W. D. (2009). Introduction to Optical Mineralogy (International ed.).